|
| 正四面体と四角錐 |
|
最近は、正四面体を作ることに興味があります。
高校の化学の中では、「不斉炭素原子」というものがあります。炭素には結合する手が4本あります。その4本にどれも異なる原子または原子の集団が結合すると、その炭素を「不斉炭素原子」と特別に名前を付けるようになります。不斉炭素原子を持つ化合物には、不思議な性質が現れてきます。それが、分子の右と左の世界です。
夏の塾では、東大の教授でいらっしゃる黒田玲子先生が本当にわかりやすく、素晴らしい授業をしてくれた世界です。6日（月曜日）の1時間目の講和
http://juku.netj.or.jp/jukumovie/ から見られます。
高校の有機化学では非常に大切な概念なので授業をしています。正四面体を教具として、簡単に作りたいと試行錯誤しています。牛乳パックを4cmの幅で切ったものを対角線に山折していくと正四面体ができるのです！実は、これは仲間とお酒を飲みながら話をしていて箸袋を折っていた時に気づいたのです。そして、授業に活用すると生徒たちも楽しんで理解してくれました。
大学受験の登竜門であるセンター試験でも有機化学の立体構造はよく出る問題なので、私の授業では自分で作成した正四面体を見ながら大学入試問題を解き、さらに理解を深めてくれています。最近は、牛乳パックを集めるのも苦労があるので、封筒からも作るようになりました。そして、折り紙（正方形）や広告（適当な長方形）からも…興味はたくさんあります。
展開図もいろいろなものができるのです。三角形のものや、台形、そして、五角形のものなどなど。自分で楽しんでいます。正四面体のアイデアノートはもうすでに1冊目を終えようとしているくらいです。
そこで、今日は今、私の中での未解決問題の一つの紹介です。解けたら是非とも教えて欲しいのです。
サイコロのような正六面体を机の上に置きます。（図1）上面の対角線に線を引きます。下面には上面とは、ひねりの位置になっているように対角線を引きます。上から見るとバツ（×）印になっていればいいのです。その上下に書いた対角線の端を結ぶように線を引くと、そこに正四面体の辺が現れます。（図2）
 |
|
 |
| 図1 |
|
図2 |
正四面体の面はすべて正三角形です。正四面体の辺は、6本です。（ちなみに、頂点は4個）この辺がすべて正六面体の面の対角線として現れるのです。
そして、正六面体の1辺をaとすると、正六面体の体積はaの三乗です。（a3）正六面体の中に現れた正四面体の体積は正六面体の3分の1ですね。（良い計算練習になりますよ！）これは、正六面体の1面を底面としてできる四角錐（ピラミッドの形）（図3）と同体積です。
 |
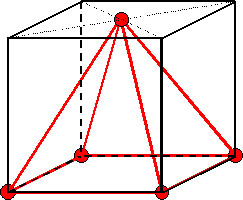| 図3 |
正四面体と四角錐は面の形も頂点や辺の数が違います。なんとか等積変形して正四面体から四角錐が作れないのでしょうか？よく切れるノコギリとノリを使って、正四面体から四角錐は作ることはできないのでしょうか？または、頂点などをうまく移動させて（もちろん、等積変形です）立体の変形は可能なのでしょうか？
数学を専門としている先生に尋ねてみたら「不可能かもしれない。」という、回答がありました。でも、その理由は詳しくはわからないようでした。
「不可能」という言葉に、今、非常に興味があります。「不可能」の証明は非常に難しいのです。もしかしたら、意外な方法で変形できるかもしれません。それは、「不可能」の証明ができるまで持つことができる知的なワクワク感だと思います。
できれば、難しい高等数学の証明でなく、普通に勉強している中学生が理解できる証明が欲しいのですが… |
 （兼龍盛・江戸川学園取手高等学校
教諭） |
|
|
 |
|
Copyright
(C) 2008 特定非営利活動法人 ネットジャーナリスト協会